
13
Mar 2023
KMeans Clustering
Akshay Iyer |
MCA
Introduction
The world of AI can simply be divided into 2 parts. Supervised where the training labels are available with the data
(Imagine a teacher teaching a student) and Unsupervised (A tadpole learning to swim) by self-inferencing of data.
Clustering belongs to the 2nd category. Clustering involves the determination of class labels based on the data given.
This acts as an input further to classification
algorithms.Clustering is NOT the same as classification which has class labels and hence is
supervised. Below we discuss about K means, a powerful partitioning-based clustering technique. Here the number of class
labels are defined at the start. (Imagine being given a long list of seemingly unrelated items and being asked to divide
them into n groups.) Seems impossible! We'll it's NOT. Let's dive into it!
KMeans is an unsupervised learning technique, Clustering involves group similar data together into classes based on the
similarities between them. The fundamental difference with respect to classification is that classification works with
labelled data. Clustering is done on unlabeled data. In fact, the output of clustering is further used with a
classification algorithm. We want to group data together that have no labels with them.
KMeans is a partitioning clustering technique, here we define the number of clusters right at the start. This raises an
important question. How can we determine the number of clusters at the start when we don’t even know the similarities,
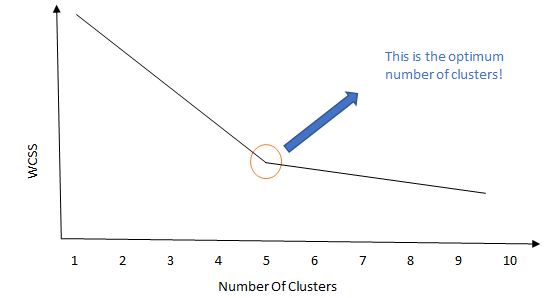
labels of the data? To do this the “elbow method” is used. In this method, we basically run the clustering algorithm
with different cluster numbers and measure the WCSS (Within Clusters Sum of Squares). The point at which there is a
sharp drop in WCSS is the optimum cluster count. Another approach is by trial and error.
Consider this example:
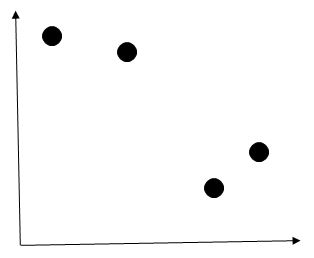
Now let us understand this algorithm with an example. Assume we have 4 points in a 2D space as below.
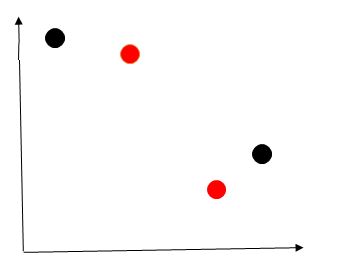
Let’s say we set the number of clusters as 2, (k = 2).
Step 1: Randomly select ‘k’ points as cluster centers.
Points in red represent the randomly selected cluster centers.
 Step 2: Compute the distance of all points from the cluster centers.
Step 2: Compute the distance of all points from the cluster centers.
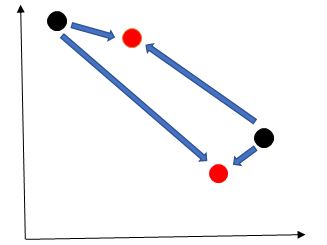
The distance is calculated using either Euclidean distance function or Manhattan (City Block) distance function.
Euclidean Distance Function:
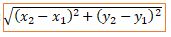
Manhattan Distance Function:
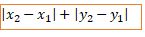
The choice of distance function is based on the type of problem, generally euclidean distance function is used.
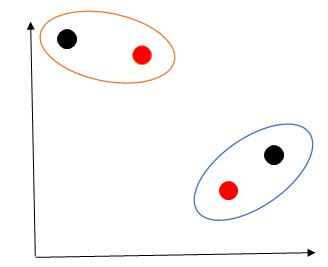
Step 3: Assign each point to the cluster center closest to it.
 Step 4: Recompute the cluster centers.
Step 4: Recompute the cluster centers.
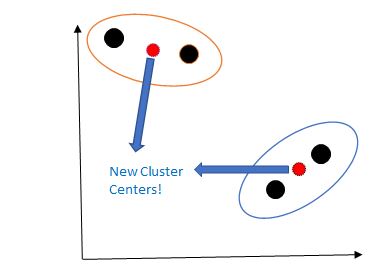 The cluster centers are recomputed by taking a mean of all points in the clusters.
The cluster centers are recomputed by taking a mean of all points in the clusters.
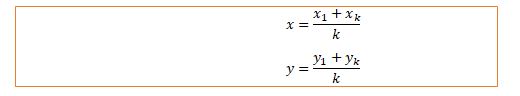
Here k refers to the number of points in the individual cluster.
Step 5: Repeat the above process till:
- Cluster Centers do not change.
- Points continue to remain in the same cluster.
- Maximum number of iterations have been reached.
This step is very critical, it signifies the termination condition for the algorithm. In rare cases we may never find
any centers that don’t change; The max iterations have a great significance here to ensure that the algorithm does
terminate.
Important Consideration.
When we execute the algorithm in real time, the following
output is generated.
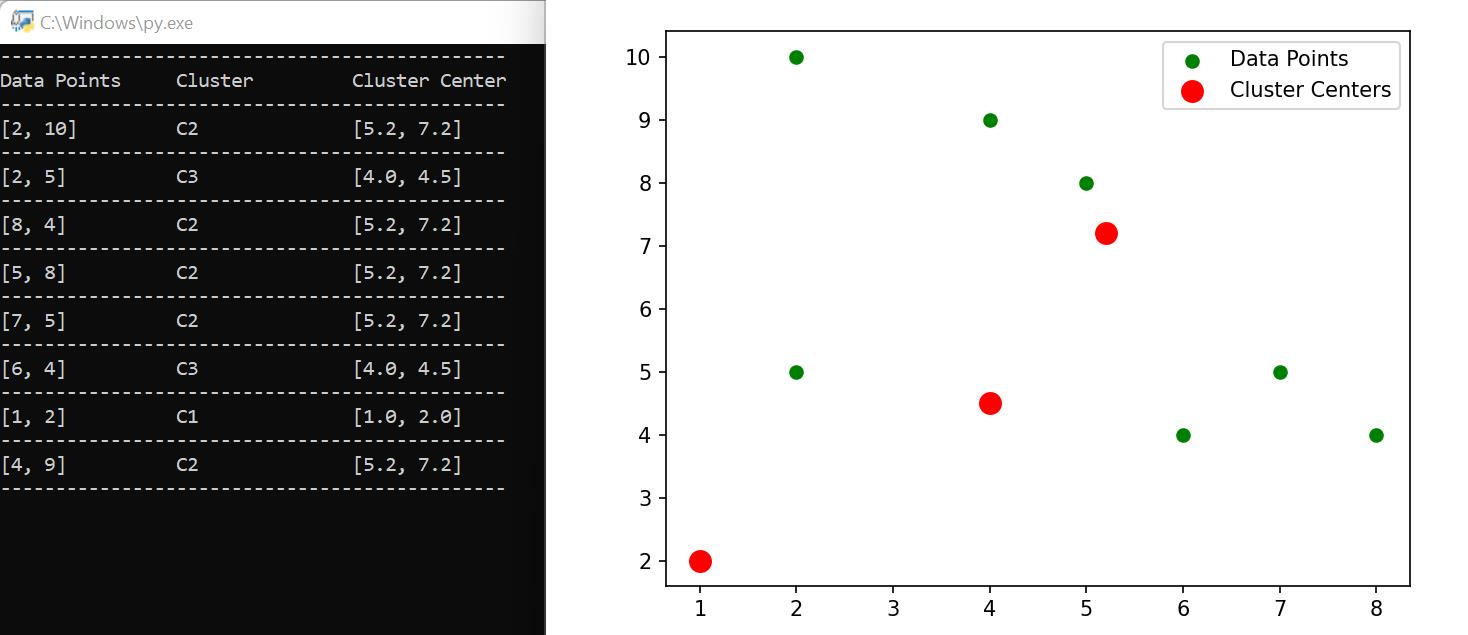
When we re-execute the same algorithm, the following output is generated.
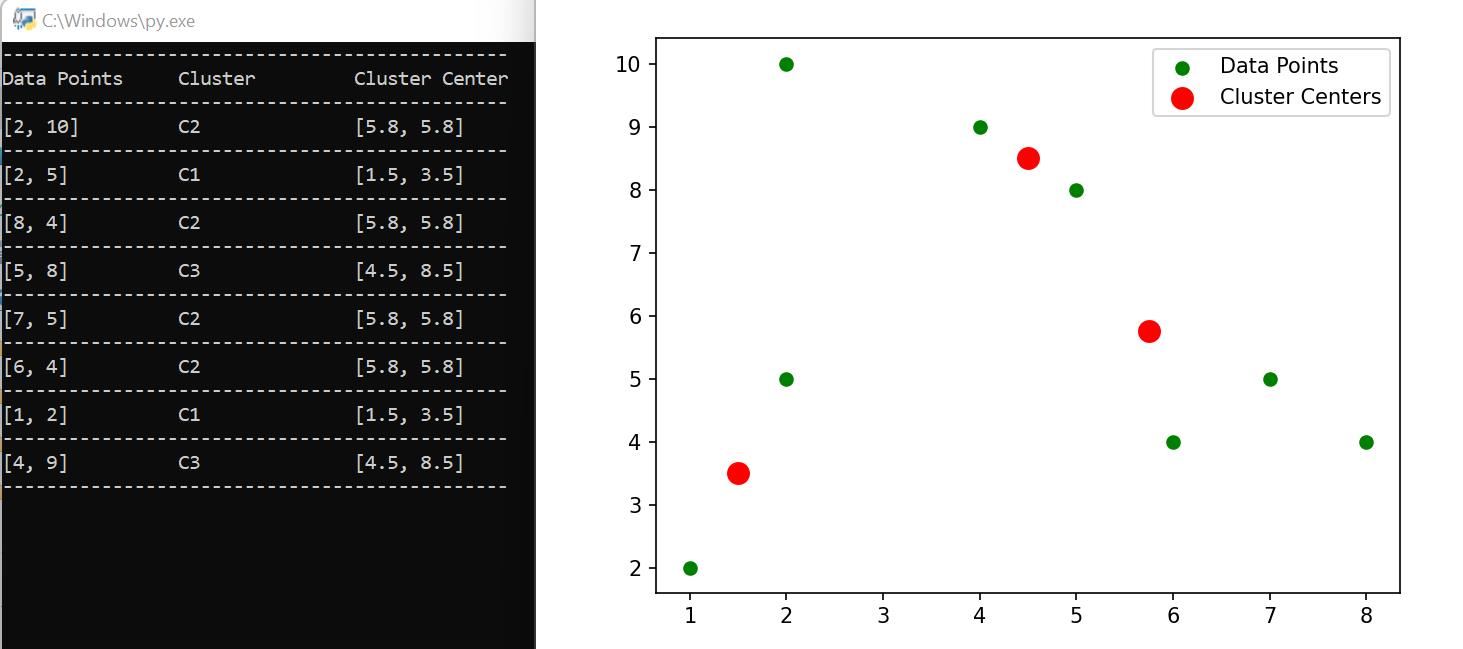
Again, on further execution, the following output is generated.
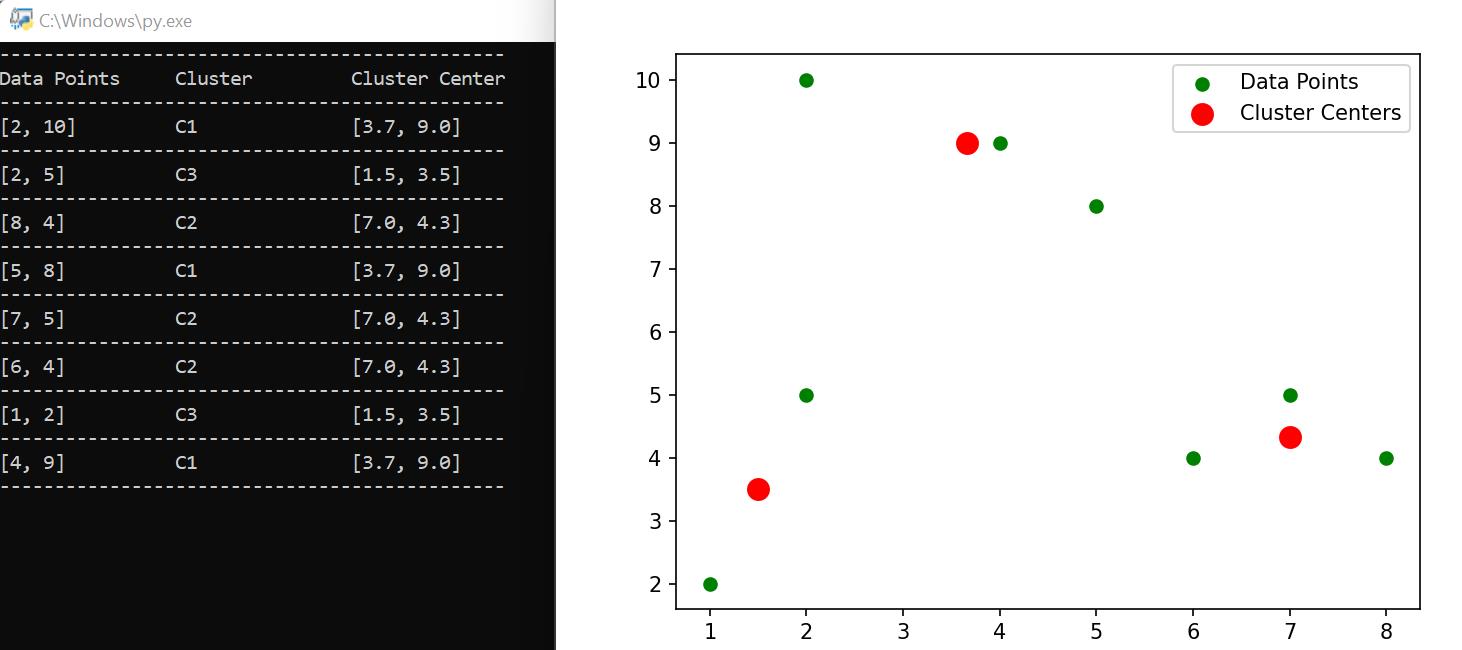
What is this behavior? Why are the clusters formed changing each run?
This is because the initial cluster centers are selected at random. This is the reason why the clusters formed change.
To overcome this issue, KMeans++ algorithm was introduced that defines a seed using which the cluster centers are
determined.
 Leave a reply
Leave a reply
 Reviews (0)
Reviews (0)
 Reviews (0)
Reviews (0)






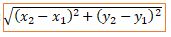
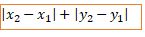


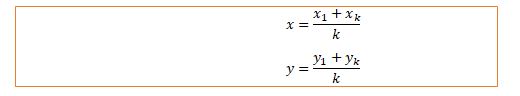



 Leave a reply
Leave a reply
 Reviews (0)
Reviews (0)
 Reviews (0)
Reviews (0)